1023. Цепные дроби

Пусть b₀, b₁, b₂, ..., b_n некоторые целые числа вида b_k > 0 для k > 0. Цепная дробь порядка n с коэффициентами b₁, b₂, ..., b_n и первоначальным целым b₀ определяется следующим выражением

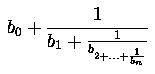
которая может быть записана в эквивалентном виде как [b₀; b₁, ..., b_n].

Например, пусть дана дробь порядка n = 3, с числами [2; 3, 1, 4]. Это эквивалентно

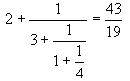
Напишите программу, которая записывает заданную рациональную дробь в виде цепной дроби. Для обеспечения уникальности необходимо, чтобы b_n > 1.

Вход. Состоит из неопределенного числа рациональных чисел. Каждое рациональное число представлено в виде дроби: числитель и знаменатель.

Выход. Для каждого рационального числа в отдельной строке выведите его соответствующее представление в виде цепной дроби.

Пример входа	Пример выхода
43 19 1 2	[2;3,1,4] [0;2]

РЕШЕНИЕ

цепные дроби

Анализ алгоритма

Дробь a / b можно записать в виде:

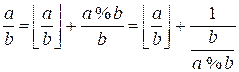
Для разложения рационального числа a / b в цепную дробь следует записать его целую часть , и далее, в случае присутствия дробной части, следует разложить в цепную дробь число b / (a % b).

Пример

= = = =

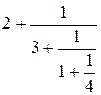
Таким образом 43 / 19 = [2; 3, 1, 4].

Реализация алгоритма

В массиве res будем строить цепную дробь.

vector<int> res;

Читаем дробь a / b.

while(scanf ("%d %d",&a,&b) == 2)

{

res.clear();

Преобразовываем дробь в цепную.

while(b != 1)

{

res.push_back(a/b);

a = a % b;

swap(a,b);

}

res.push_back(a);

Выводим цепную дробь, соответствующую a / b.

printf("[%d;%d",res[0],res[1]);

for(i = 2; i < res.size(); i++)

printf(",%d",res[i]);

printf("]\n");

}